Checking Existence of Edge Length Limited Paths
Leetcode Daily Challenge (29th April, 2023)
Problem Statement:-
An undirected graph of n nodes is defined by edgeList, where edgeList[i] = [u<sub>i</sub>, v<sub>i</sub>, dis<sub>i</sub>] denotes an edge between nodes u<sub>i</sub> and v<sub>i</sub> with distance dis<sub>i</sub>. Note that there may be multiple edges between two nodes.
Given an array queries, where queries[j] = [p<sub>j</sub>, q<sub>j</sub>, limit<sub>j</sub>], your task is to determine for each queries[j] whether there is a path between p<sub>j</sub> and q<sub>j</sub> such that each edge on the path has a distance strictly less than limit<sub>j</sub> .
Return a boolean array answer, where answer.length == queries.length and the j<sup>th</sup> value of answer is true if there is a path for queries[j] is true, and false otherwise.
Link: https://leetcode.com/problems/checking-existence-of-edge-length-limited-paths/description/
Problem Explanation with examples:-
Example 1
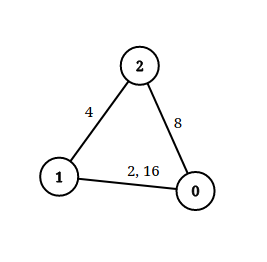
Input: n = 3, edgeList = [[0,1,2],[1,2,4],[2,0,8],[1,0,16]], queries = [[0,1,2],[0,2,5]]
Output: [false,true]
Explanation: The above figure shows the given graph. Note that there are two overlapping edges between 0 and 1 with distances 2 and 16.
For the first query, between 0 and 1 there is no path where each distance is less than 2, thus we return false for this query.
For the second query, there is a path (0 -> 1 -> 2) of two edges with distances less than 5, thus we return true for this query.
Example 2
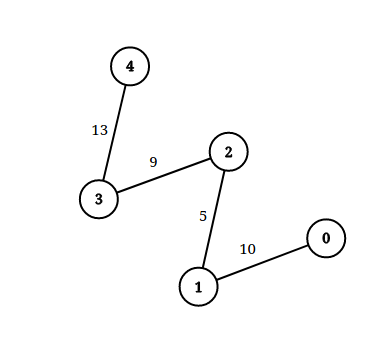
Input: n = 5, edgeList = [[0,1,10],[1,2,5],[2,3,9],[3,4,13]], queries = [[0,4,14],[1,4,13]]
Output: [true,false]
Exaplanation: The above figure shows the given graph.
Constraints
2 <= n <= 10<sup>5</sup>1 <= edgeList.length, queries.length <= 10<sup>5</sup>edgeList[i].length == 3queries[j].length == 30 <= u<sub>i</sub>, v<sub>i</sub>, p<sub>j</sub>, q<sub>j</sub> <= n - 1u<sub>i</sub> != v<sub>i</sub>p<sub>j</sub> != q<sub>j</sub>1 <= dis<sub>i</sub>, limit<sub>j</sub> <= 10<sup>9</sup>There may be multiple edges between two nodes.
Intuition:-
The problem at hand involves checking if a path exists between two nodes in an undirected graph, where the weight of each edge on the path is less than or equal to a given limit.
One way to approach this problem is to use the Union-Find data structure to process the edges in the graph in increasing order of weight. If the endpoints of an edge are not already connected, we merge them, as adding the edge between them would result in a cycle, which cannot be included in a valid path.
We can then process the queries in increasing order of the limit and check if the two endpoints of each query are connected. If they are, then a path exists between them, with all edges having weights less than or equal to the current limit.
Solution:-
First, we sort the queries based on the limit in ascending order.
Next, we sort the edges based on the weight in ascending order.
Traverse the queries and for each query, we traverse the edges and union the nodes if the weight of the edge is less than the limit of the query.
Finally, we check if the nodes are connected or not and store the result in the answer array.
Return the answer array.
Code:-
JAVA Solution
class UnionFind {
int[] parent;
int[] rank;
public UnionFind(int n) {
parent = new int[n];
rank = new int[n];
for (int i = 0; i < n; i++) {
parent[i] = i;
rank[i] = 0;
}
}
public int find(int x) {
if (parent[x] != x) {
parent[x] = find(parent[x]);
}
return parent[x];
}
public void union(int x, int y) {
int px = find(x), py = find(y);
if (px != py) {
if (rank[px] < rank[py]) {
parent[px] = py;
} else if (rank[px] > rank[py]) {
parent[py] = px;
} else {
parent[py] = px;
rank[px]++;
}
}
}
public boolean connected(int x, int y) {
return find(x) == find(y);
}
}
class Solution {
public boolean[] distanceLimitedPathsExist(int n, int[][] edges, int[][] queries) {
boolean[] ans = new boolean[queries.length];
for (int i = 0; i < queries.length; i++) {
queries[i] = new int[]{queries[i][0], queries[i][1], queries[i][2], i};
}
Arrays.sort(queries, (a, b) -> Integer.compare(a[2], b[2]));
Arrays.sort(edges, (a, b) -> Integer.compare(a[2], b[2]));
UnionFind uf = new UnionFind(n);
int i = 0;
for (int[] q : queries) {
int u = q[0], v = q[1], limit = q[2], qid = q[3];
while (i < edges.length && edges[i][2] < limit) {
uf.union(edges[i][0], edges[i][1]);
i++;
}
ans[qid] = uf.connected(u, v);
}
return ans;
}
}
Python Solution
class UnionFind:
def __init__(self, n):
self.parent = list(range(n))
self.rank = [0] * n
def find(self, x):
if self.parent[x] != x:
self.parent[x] = self.find(self.parent[x])
return self.parent[x]
def union(self, x, y):
px, py = self.find(x), self.find(y)
if px != py:
if self.rank[px] < self.rank[py]:
self.parent[px] = py
elif self.rank[px] > self.rank[py]:
self.parent[py] = px
else:
self.parent[py] = px
self.rank[px] += 1
def connected(self, x, y):
return self.find(x) == self.find(y)
class Solution:
def distanceLimitedPathsExist(self, n: int, edges: List[List[int]], queries: List[List[int]]) -> List[bool]:
edges = sorted(edges, key=lambda x: x[2])
ans = [False] * len(queries)
uf = UnionFind(n)
i = 0
sorted_queries = sorted(enumerate(queries), key=lambda x: x[1][2])
for q_idx, (u, v, limit) in sorted_queries:
while i < len(edges) and edges[i][2] < limit:
uf.union(edges[i][0], edges[i][1])
i += 1
ans[q_idx] = uf.connected(u, v)
return ans
Complexity Analysis:-
TIME:-
The time complexity of the Union-Find data structure is O(alpha(n)), where alpha is the inverse Ackermann function, which grows very slowly and is considered to be almost constant.
In the distanceLimitedPathsExist function, we first sort the edges in O(m log m) time, where m is the number of edges in the graph. Then, we sort the queries in O(q log q) time, where q is the number of queries. For each query, we perform at most m operations on the Union-Find data structure. Therefore, the overall time complexity of the function is O((m + q) alpha(n) log n).
SPACE:-
The space complexity of the Union-Find data structure is O(n). In the distanceLimitedPathsExist function, we use additional space to store the sorted edges and queries, as well as the answer array. Therefore, the overall space complexity of the function is O((m + q) + n).
