Equal Row and Column Pairs

Problem Statement:-

Given a 0-indexed n x n integer matrix grid, return the number of pairs (r<sub>i</sub>, c<sub>j</sub>) such that row r<sub>i</sub> and column c<sub>j</sub> are equal.

A row and column pair is considered equal if they contain the same elements in the same order (i.e., an equal array).

Link: https://leetcode.com/problems/equal-row-and-column-pairs/description/

Problem Explanation with examples:-

Example 1

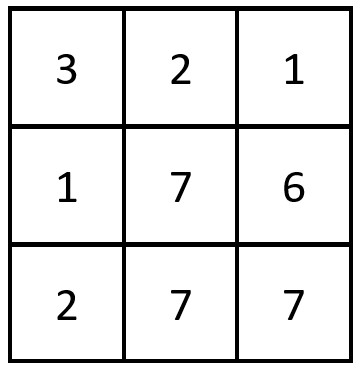
Input: grid = [[3,2,1],[1,7,6],[2,7,7]]
Output: 1
Explanation: There is 1 equal row and column pair:
- (Row 2, Column 1): [2,7,7]

Example 2

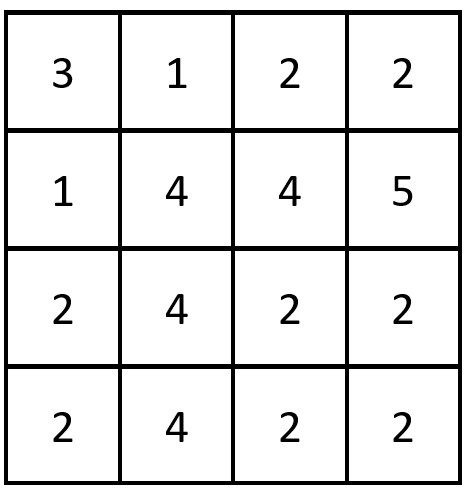
Input: grid = [[3,1,2,2],[1,4,4,5],[2,4,2,2],[2,4,2,2]]
Output: 3
Explanation: There are 3 equal row and column pairs:
- (Row 0, Column 0): [3,1,2,2]
- (Row 2, Column 2): [2,4,2,2]
- (Row 3, Column 2): [2,4,2,2]

Constraints

• n == grid.length == grid[i].length

• 1 <= n <= 200

• 1 <= grid[i][j] <= 10<sup>5</sup>

Intuition:-

• We will create a transpose of the grid and check each row of grid against each row of the transpose. If they are equal, then we have found a pair of equal rows.

Solution:-

• Create the transpose of the grid and store it in a variable res.

• Initialize a variable c to store the count of equal pairs. Set it to 0.

• Iterate over the rows of grid. For each row, iterate over the rows of res. If the row of grid is equal to the row of res, then increment c by 1.

• Return c.

Code:-

JAVA Solution

class Solution {
    public int equalPairs(List<List<Integer>> grid) {
        List<List<Integer>> res = new ArrayList<>();
        for (int i = 0; i < grid.get(0).size(); i++) {
            List<Integer> column = new ArrayList<>();
            for (int j = 0; j < grid.size(); j++) {
                column.add(grid.get(j).get(i));
            }
            res.add(column);
        }

        int count = 0;
        for (List<Integer> row : grid) {
            for (List<Integer> column : res) {
                if (row.equals(column)) {
                    count++;
                }
            }
        }
        return count;
    }
}

Python Solution

class Solution:
    def equalPairs(self, grid: List[List[int]]) -> int:
        res = [[grid[j][i] for j in range(len(grid))] for i in range(len(grid[0]))]
        c = 0
        for i in grid:
            for j in res:
                if i == j:
                    c += 1
        return c

Complexity Analysis:-

TIME:-

The time complexity is O(n^2). The outer loop iterates over each row of the grid, and the nested loops iterate over each column in res for every row in grid.

SPACE:-

The space complexity is O(n^2), as we create a new matrix res to store the transposed elements of the grid matrix.

References:-

• 2D Arrays

Connect with me:-

• Twitter

• Github

• LinkedIn