Is Graph Bipartite?

Problem Statement:-

There is an undirected graph with n nodes, where each node is numbered between 0 and n - 1. You are given a 2D array graph, where graph[u] is an array of nodes that node u is adjacent to. More formally, for each v in graph[u], there is an undirected edge between node u and node v. The graph has the following properties:

• There are no self-edges (graph[u] does not contain u).

• There are no parallel edges (graph[u] does not contain duplicate values).

• If v is in graph[u], then u is in graph[v] (the graph is undirected).

• The graph may not be connected, meaning there may be two nodes u and v such that there is no path between them.

A graph is bipartite if the nodes can be partitioned into two independent sets A and B such that every edge in the graph connects a node in set A and a node in set B.

Return true if and only if it is bipartite.

Link: https://leetcode.com/problems/is-graph-bipartite/description/

Problem Explanation with examples:-

Example 1

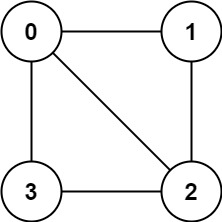
Input: graph = [[1,2,3],[0,2],[0,1,3],[0,2]]
Output: false
Explanation: There is no way to partition the nodes into two independent sets such that every edge connects a node in one and a node in the other.

Example 2

Input: graph = [[1,3],[0,2],[1,3],[0,2]]
Output: true
Explanation: We can partition the nodes into two sets: {0, 2} and {1, 3}.

Constraints

• graph.length == n

• 1 <= n <= 100

• 0 <= graph[u].length < n

• 0 <= graph[u][i] <= n - 1

• graph[u] does not contain u.

• All the values of graph[u] are unique.

• If graph[u] contains v, then graph[v] contains u.

Intuition:-

• A graph is bipartite if and only if it is 2-colorable.

• We try to color each node with a color, if we can't, then it is not bipartite.

• We use dfs to color each node.

Solution:-

• Create a list of colors of length n, where n is the number of nodes initialized to 0.

• Define a dfs function that takes in the graph, colors, node, and color.

• If the color of the node is not 0, then return whether the color of the node is the same as the color passed in.

• Set the color of the node to the color passed in.

• For each neighbor of the node, if the dfs function returns false, then return false.

• Else, return true.

• After the function, iterate through each node in the graph and if the color of the node is 0, then call the dfs function on the node and if it returns false, then return false.

• Else, return true.

Code:-

JAVA Solution

class Solution {
    public boolean isBipartite(int[][] graph) {
        int n = graph.length;
        int[] colors = new int[n];

        for (int i = 0; i < n; i++) {
            if (colors[i] == 0) {
                if (!dfs(graph, colors, i, 1)) {
                    return false;
                }
            }
        }

        return true;
    }

    private boolean dfs(int[][] graph, int[] colors, int node, int color) {
        if (colors[node] != 0) {
            return colors[node] == color;
        }

        colors[node] = color;

        for (int neighbor : graph[node]) {
            if (!dfs(graph, colors, neighbor, -color)) {
                return false;
            }
        }

        return true;
    }
}

Python Solution

class Solution:
    def isBipartite(self, graph: List[List[int]]) -> bool:
        n = len(graph)
        colors = [0] * n
        def dfs(graph, colors, node, color):
            if colors[node] != 0:
                return colors[node] == color

            colors[node] = color

            for neighbor in graph[node]:
                if not dfs(graph, colors, neighbor, -color):
                    return False

            return True

        for i in range(n):
            if colors[i] == 0:
                if not dfs(graph, colors, i, 1):
                    return False

        return True

Complexity Analysis:-

TIME:-

The time complexity is O(V + E) where V is the number of vertices and E is the number of edges. We visit each node once and each edge once in the worst case.

SPACE:-

The space complexity is O(V) where V is the number of vertices. We use a list of colors of length V and the call stack can go as deep as V.

References:-

• Graph

• DFS

Connect with me:-

• Twitter

• Github

• LinkedIn