Maximum Width of Binary Tree
Leetcode Daily Challenge (20th April, 2023)
Problem Statement:-
Given the root of a binary tree, return the maximum width of the given tree.
The maximum width of a tree is the maximum width among all levels.
The width of one level is defined as the length between the end-nodes (the leftmost and rightmost non-null nodes), where the null nodes between the end-nodes that would be present in a complete binary tree extending down to that level are also counted into the length calculation.
It is guaranteed that the answer will in the range of a 32-bit signed integer.
Link: https://leetcode.com/problems/maximum-width-of-binary-tree/description/
Problem Explanation with examples:-
Example 1
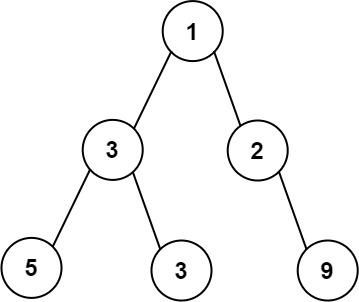
Input: root = [1,3,2,5,3,null,9]
Output: 4
Explanation: The maximum width exists in the third level with length 4 (5,3,null,9).
Example 2
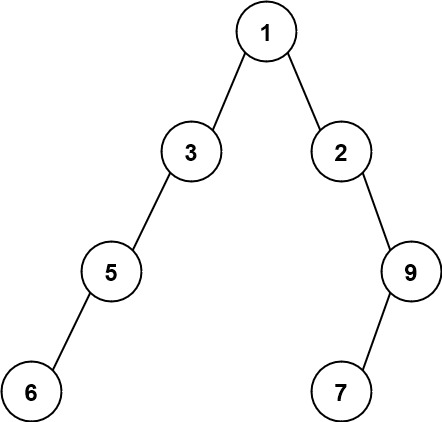
Input: root = [1,3,2,5,null,null,9,6,null,7]
Output: 7
Explanation: The maximum width exists in the fourth level with length 7 (6,null,null,null,null,null,7).
Example 3
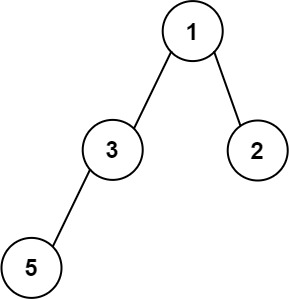
Input: root = [1,3,2,5]
Output: 2
Explanation: The maximum width exists in the second level with length 2 (3,2).
Constraints
The number of nodes in the tree is in the range
[1, 3000].-100 <= Node.val <= 100
Intuition:-
BFS will be used to traverse the tree level by level.
The width of the tree at a level is the difference between the last node and the first node.
The first node is the node that is encountered first at a level.
The last node is the node that is encountered last at a level.
ans variable will be used to store the maximum width of the tree.
We don't need the node values so we will store the ordered nodes numbers in the nodes.
Solution:-
Initialize ans to 0.
Initialize a queue with the root node, its number and level. The root node will have number 1 and level 0.
Initialize prevLvl to 0 and prevNum to 1.
While the queue is not empty:
Pop the first node from the queue.
If the level of the node is greater than the previous level:
Update prevLvl to the current level. Update prevNum to the current node number.
Update ans to the maximum of ans and the difference between the current node number and the previous node number.
If the left child of the node is not null, append it to the queue with its number, 2*current node number and level+1.
If the right child of the node is not null, append it to the queue with its number, 2*current node number+1 and level+1.
Return ans.
Code:-
JAVA Solution
class Solution {
public int widthOfBinaryTree(TreeNode root) {
Deque<TreeNode> queue=new ArrayDeque<>();
root.val=0;
queue.add(root);
return bfs(queue);
}
public int bfs(Deque<TreeNode> queue){
int maxWidth = 1;
while(!queue.isEmpty()){
int s=queue.size();
int left = queue.peek().val;
int right = left;
for(int i=0;i<s;i++){
TreeNode node=queue.removeFirst();
if(node.left!=null){
node.left.val = node.val * 2 - 1;
queue.add(node.left);
}
if(node.right!=null){
node.right.val = node.val * 2;
queue.add(node.right);
}
if(i==s-1)
right=node.val;
}
maxWidth=Math.max(maxWidth,right-left+1);
}
return maxWidth;
}
}
Python Solution
class Solution:
def widthOfBinaryTree(self, root: Optional[TreeNode]) -> int:
ans = 0
q = deque([[root,1,0]])
prevLvl = 0
prevNum = 1
while q:
node, num, lvl = q.popleft()
if lvl > prevLvl:
prevLvl = lvl
prevNum = num
ans = max(ans, num - prevNum + 1)
if node.left:
q.append([node.left, 2*num, lvl+1])
if node.right:
q.append([node.right, 2*num+1, lvl+1])
return ans
Complexity Analysis:-
TIME:-
The time complexity of the given Python code is O(n) where n is the number of nodes in the tree. We will traverse the tree once.
SPACE:-
The space complexity of the code is also O(n) where n is the number of nodes in the tree. We will store the nodes in the queue.
