Remove Max Number of Edges to Keep Graph Fully Traversable
Leetcode Daily Challenge (30th April, 2023)
Problem Statement:-
Alice and Bob have an undirected graph of n nodes and three types of edges:
Type 1: Can be traversed by Alice only.
Type 2: Can be traversed by Bob only.
Type 3: Can be traversed by both Alice and Bob.
Given an array edges where edges[i] = [type<sub>i</sub>, u<sub>i</sub>, v<sub>i</sub>] represents a bidirectional edge of type type<sub>i</sub> between nodes u<sub>i</sub> and v<sub>i</sub>, find the maximum number of edges you can remove so that after removing the edges, the graph can still be fully traversed by both Alice and Bob. The graph is fully traversed by Alice and Bob if starting from any node, they can reach all other nodes.
Return the maximum number of edges you can remove, or return -1 if Alice and Bob cannot fully traverse the graph.
Problem Explanation with examples:-
Example 1
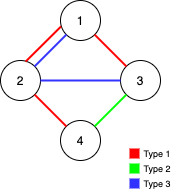
Input: n = 4, edges = [[3,1,2],[3,2,3],[1,1,3],[1,2,4],[1,1,2],[2,3,4]]
Output: 2
Explanation: If we remove the 2 edges [1,1,2] and [1,1,3]. The graph will still be fully traversable by Alice and Bob. Removing any additional edge will not make it so. So the maximum number of edges we can remove is 2.
Example 2
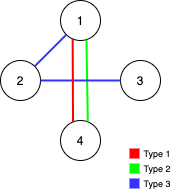
Input: n = 4, edges = [[3,1,2],[3,2,3],[1,1,4],[2,1,4]]
Output: 0
Explanation: Notice that removing any edge will not make the graph fully traversable by Alice and Bob.
Example 3
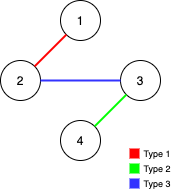
Input: n = 4, edges = [[3,2,3],[1,1,2],[2,3,4]]
Output: -1
Explanation: In the current graph, Alice cannot reach node 4 from the other nodes. Likewise, Bob cannot reach 1. Therefore it's impossible to make the graph fully traversable.
Constraints
1 <= n <= 10<sup>5</sup>1 <= edges.length <= min(10<sup>5</sup>, 3 * n * (n - 1) / 2)edges[i].length == 31 <= type<sub>i</sub> <= 31 <= u<sub>i</sub> < v<sub>i</sub> <= nAll tuples
(type<sub>i</sub>, u<sub>i</sub>, v<sub>i</sub>)are distinct.
Intuition:-
The problem requires finding the maximum number of edges that can be removed from a graph while still allowing both Alice and Bob to construct a spanning tree, which must include all nodes in the graph. The union-find data structure can be used to keep track of which nodes are connected to each other. Each node initially represents its own set.
We start by examining the edges that can be used by both Alice and Bob, also known as type 3 edges. If we can merge two nodes successfully using such an edge, then both Alice and Bob can use that edge to construct their respective spanning trees. In this case, we increment the edge count for both Alice and Bob. If the merge is unsuccessful, then we increment the rejected edge count.
We then consider the edges that can only be used by Alice or Bob, also known as type 1 and type 2 edges. If we can successfully merge two nodes using a type 1 or type 2 edge, we know that only Alice or Bob can use that edge to construct their respective spanning tree. In this case, we increment the edge count for that user. If the merge is unsuccessful, we increment the rejected edge count.
After all edges have been processed, we check whether both Alice and Bob were able to construct a spanning tree by using n-1 edges. If they both did, we return the number of rejected edges. Otherwise, we return -1.
Solution:-
First, we create two separate union find data structures for Alice and Bob.
Next, we traverse the edges and union the nodes if the type of the edge is 3. For each such union, we increment the number of edges for Alice and Bob by 1. If union is not possible, we increment the rejected edges by 1.
Next, we traverse the edges and union the nodes if the type of the edge is 1. For each such union, we increment the number of edges for Alice by 1. If union is not possible, we increment the rejected edges by 1.
Next, we traverse the edges and union the nodes if the type of the edge is 2. For each such union, we increment the number of edges for Bob by 1. If union is not possible, we increment the rejected edges by 1.
Finally, we check if the number of edges for Alice and Bob is equal to n - 1. If yes, we return the rejected edges. Else, we return -1.
Code:-
JAVA Solution
class Solution {
public int maxNumEdgesToRemove(int n, int[][] edges) {
int[] rootA = new int[n + 1];
int[] rootB = new int[n + 1];
for (int i = 1; i <= n; i++) {
rootA[i] = i;
rootB[i] = i;
}
int res = 0;
int aliceEdges = 0;
int bobEdges = 0;
for (int[] edge : edges) {
if (edge[0] == 3) {
if (union(edge[1], edge[2], rootA)) {
aliceEdges++;
if (union(edge[1], edge[2], rootB)) {
bobEdges++;
}
} else {
res++;
}
}
}
int[] rootA_copy = rootA.clone();
for (int[] edge : edges) {
if (edge[0] == 1) {
if (union(edge[1], edge[2], rootA)) {
aliceEdges++;
} else {
res++;
}
}
}
for (int[] edge : edges) {
if (edge[0] == 2) {
if (union(edge[1], edge[2], rootB)) {
bobEdges++;
} else {
res++;
}
}
}
return (aliceEdges == bobEdges && aliceEdges == n - 1) ? res : -1;
}
public boolean union(int a, int b, int[] root) {
int rootA = find(a, root);
int rootB = find(b, root);
if (rootA == rootB) {
return false;
}
root[rootA] = rootB;
return true;
}
public int find(int a, int[] root) {
if (root[a] != a) {
root[a] = find(root[a], root);
}
return root[a];
}
}
Python Solution
class Solution:
def maxNumEdgesToRemove(self, n, edges):
def find(i, root):
if i != root[i]:
root[i] = find(root[i], root)
return root[i]
def uni(x, y, root):
x, y = find(x, root), find(y, root)
if x == y: return 0
root[x] = y
return 1
res = alice_edges = bob_edges = 0
root = list(range(n + 1))
for t, i, j in edges:
if t == 3:
if uni(i, j, root):
alice_edges += 1
bob_edges += 1
else:
res += 1
root0 = root[:]
for t, i, j in edges:
if t == 1:
if uni(i, j, root):
alice_edges += 1
else:
res += 1
root = root0
for t, i, j in edges:
if t == 2:
if uni(i, j, root):
bob_edges += 1
else:
res += 1
return res if alice_edges == bob_edges == n - 1 else -1
Complexity Analysis:-
TIME:-
The function uses the union-find algorithm to keep track of the connected components of the graph. The time complexity of the find operation in the union-find algorithm is approximately O(1), and the time complexity of the uni operation is also O(1) on average. The function iterates over the edges three times, with each iteration taking O(m) time, where m is the number of edges in the graph. Therefore, the total time complexity of the function is O(m).
SPACE:-
The function uses a list root of length n+1 to store the parent of each node in the union-find algorithm, so the space complexity of the function is O(n). The function also uses some variables to store the number of edges added by Alice and Bob, which take constant space. Therefore, the total space complexity of the function is O(n).
