Count Unreachable Pairs of Nodes in an Undirected Graph
Leetcode Daily Challenge (25th March, 2023)
Problem Statement:-
You are given an integer n. There is an undirected graph with n nodes, numbered from 0 to n - 1. You are given a 2D integer array edges where edges[i] = [a<sub>i</sub>, b<sub>i</sub>] denotes that there exists an undirected edge connecting nodes a<sub>i</sub> and b<sub>i</sub>.
Return the number of pairs of different nodes that are unreachable from each other.
Link: https://leetcode.com/problems/count-unreachable-pairs-of-nodes-in-an-undirected-graph/description/
Problem Explanation with examples:-
Example 1
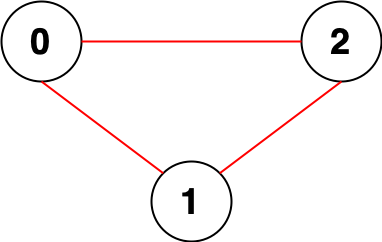
Input: n = 6, connections = [[0,1],[1,3],[2,3],[4,0],[4,5]]
Output: 3
Explanation: Change the direction of edges show in red such that each node can reach the node 0 (capital).
Example 2
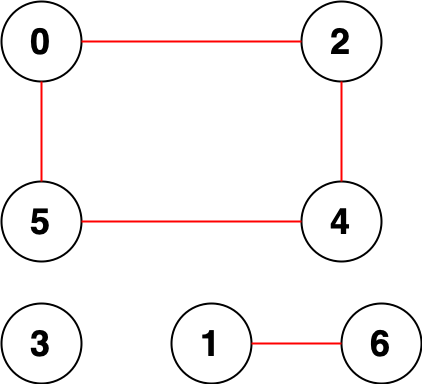
Input: n = 5, connections = [[1,0],[1,2],[3,2],[3,4]]
Output: 2
Explanation: Change the direction of edges show in red such that each node can reach the node 0 (capital).
Constraints
1 <= n <= 10<sup>5</sup>0 <= edges.length <= 2 * 10<sup>5</sup>edges[i].length == 20 <= a<sub>i</sub>, b<sub>i</sub> < na<sub>i</sub> != b<sub>i</sub>There are no repeated edges.
Intuition:-
We need to find the number of pairs of nodes that are connected by exactly one path.
We can use union find to find the number of connected components.
We can use a parent array to keep track of the parent of each node.
A rank array can be used to keep track of the rank of each node.
And a find function can be used to find the parent of a node.
We can use a makeUnion function to merge two nodes.
The connected components can be found by iterating through the edges and calling the makeUnion function on each edge.
Component members can be found by iterating through the parent array and finding the parent of each node.
The number of pairs can be found by iterating through the component members and finding the number of pairs for each component.
The number of pairs for each component can be found by multiplying the number of members in the component by the remaining members.
The remaining members can be found by subtracting the number of members in the component from the total number of nodes.
The total number of pairs can be found by adding the number of pairs for each component.
Solution:-
Initialize a parent array to keep track of the parent of each node and set all the elements to the index of the element.
Initialize a rank array to keep track of the rank of each node and set all the elements to 0.
Iterate through the edges and call the makeUnion function on each edge.
Initialize a componentMembers array to keep track of the number of members in each component and set all the elements to 0.
Iterate through the parent array and find the parent of each node.
Increment the componentMembers array at the index of the parent by 1.
Initialize a pairs variable to keep track of the number of pairs and set it to 0.
Initialize a remainingMemebers variable to keep track of the number of remaining members and set it to the total number of nodes.
Iterate through the componentMembers array.
If the current element is 0, continue.
Set the currentComponents variable to the current element.
Decrement the remainingMemebers variable by the currentComponents variable.
Set the currentPairs variable to the product of the currentComponents variable and the remainingMemebers variable.
Increment the pairs variable by the currentPairs variable.
Return the pairs variable.
Code:-
JAVA Solution
class Solution {
int[] parent;
int[] rank;
int find(int x){
while(parent[x]!=x){
x = parent[parent[x]];
}
return x;
}
void makeUnion(int x, int y){
int xPar = find(x);
int yPar = find(y);
if(xPar == yPar){
return;
}
else if(rank[xPar]<rank[yPar]){
parent[xPar] = yPar;
}
else if(rank[xPar]>rank[yPar]){
parent[yPar] = xPar;
}
else{
parent[yPar] = xPar;
rank[xPar]++;
}
return;
}
public long countPairs(int n, int[][] edges) {
parent = new int[n];
rank = new int[n];
for(int i=0; i<n; i++){
parent[i] = i;
}
for(int[] edge:edges){
makeUnion(edge[0], edge[1]);
}
long[] componentMembers = new long[n];
for(int i=0; i<n; i++){
int par = find(i);
componentMembers[par]++;
}
long pairs = 0;
long remainingMemebers = n;
for(int i=0; i<n; i++){
if(componentMembers[i]==0){
continue;
}
long currentComponents = componentMembers[i];
remainingMemebers -= currentComponents;
long currentPairs = currentComponents * remainingMemebers;
pairs+=currentPairs;
}
return pairs;
}
}
Python Solution
class Solution:
def __init__(self):
self.parent = []
self.rank = []
def find(self, x: int) -> int:
while self.parent[x] != x:
x = self.parent[self.parent[x]]
return x
def makeUnion(self, x: int, y: int) -> None:
xPar = self.find(x)
yPar = self.find(y)
if xPar == yPar:
return
elif self.rank[xPar] < self.rank[yPar]:
self.parent[xPar] = yPar
elif self.rank[xPar] > self.rank[yPar]:
self.parent[yPar] = xPar
else:
self.parent[yPar] = xPar
self.rank[xPar] += 1
def countPairs(self, n: int, edges: List[List[int]]) -> int:
self.parent = [i for i in range(n)]
self.rank = [0] * n
for edge in edges:
self.makeUnion(edge[0], edge[1])
componentMembers = [0] * n
for i in range(n):
par = self.find(i)
componentMembers[par] += 1
pairs = 0
remainingMemebers = n
for i in range(n):
if componentMembers[i] == 0:
continue
currentComponents = componentMembers[i]
remainingMemebers -= currentComponents
currentPairs = currentComponents * remainingMemebers
pairs += currentPairs
return pairs
Complexity Analysis:-
TIME:-
The time complexity of the find() function is O(logn) and the time complexity of the makeUnion() function is O(1) amortized time using the union by rank and path compression heuristics. The loop that counts the number of members in each component takes O(n) time. The loop that computes the number of pairs takes O(n) time. Therefore, the overall time complexity is O(nlogn).
SPACE:-
The space complexity is O(n) since we need to store the parent and rank arrays, as well as the componentMembers array.
