Longest Cycle in a Graph
Leetcode Daily Challenge (26th March, 2023)
Problem Statement:-
You are given a directed graph of n nodes numbered from 0 to n - 1, where each node has at most one outgoing edge.
The graph is represented with a given 0-indexed array edges of size n, indicating that there is a directed edge from node i to node edges[i]. If there is no outgoing edge from node i, then edges[i] == -1.
Return the length of the longest cycle in the graph. If no cycle exists, return -1.
A cycle is a path that starts and ends at the same node.
Link: https://leetcode.com/problems/longest-cycle-in-a-graph/description/
Problem Explanation with examples:-
Example 1
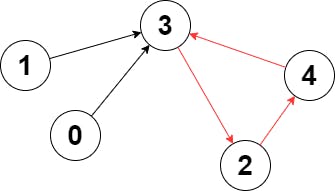
Input: edges = [3,3,4,2,3]
Output: 3
Explanation: The longest cycle in the graph is the cycle: 2 -> 4 -> 3 -> 2.
The length of this cycle is 3, so 3 is returned.
Example 2

Input: edges = [2,-1,3,1]
Output: -1
Explanation: There are no cycles in this graph.
Constraints
n == edges.length2 <= n <= 10<sup>5</sup>-1 <= edges[i] < nedges[i] != i
Intuition:-
We need to find the length of the longest cycle in the graph.
We can use a node_visited_at_time array to keep track of the time step at which each node was visited.
Another variable can be used to keep track of the current time step.
Then we can iterate through the nodes and find the length of the longest cycle for each node.
The time step at which the node was visited can be updated by using the time_step variable.
The time_step variable will be incremented by 1 after each node is visited.
The length of the longest cycle for each node can be found by iterating through the nodes in the cycle and finding the difference between the current time step and the time step at which the node was visited.
Solution:-
Initialize a variable longest_cycle_len to -1 to keep track of the length of the longest cycle.
Initialize a variable time_step to 1 to keep track of the current time step.
Initialize a node_visited_at_time array to keep track of the time step at which each node was visited and set all the elements to 0.
Iterate through the nodes.
If the current node was visited, continue.
Else, initialize a start_time variable to the current time step.
Initialize a u variable to the current node.
While u is not -1 and the node at the index of u in the node_visited_at_time array is 0, update the node_visited_at_time array at the index of u to the current time step and increment the time_step variable by 1 and update the u variable to the node at the index of u in the edges array.
If u is not -1 and the node at the index of u in the node_visited_at_time array is greater than or equal to the start_time variable, update the longest_cycle_len variable to the maximum of the longest_cycle_len variable and the difference between the current time step and the node at the index of u in the node_visited_at_time array.
Return the longest_cycle_len variable.
Code:-
JAVA Solution
class Solution {
public int longestCycle(int[] edges) {
int longest_cycle_len = -1;
int time_step = 1;
int[] node_visited_at_time = new int[edges.length];
for (int current_node = 0; current_node < edges.length; current_node++) {
if (node_visited_at_time[current_node] > 0) {
continue;
}
int start_time = time_step;
int u = current_node;
while (u != -1 && node_visited_at_time[u] == 0) {
node_visited_at_time[u] = time_step;
time_step++;
u = edges[u];
}
if (u != -1 && node_visited_at_time[u] >= start_time) {
longest_cycle_len = Math.max(longest_cycle_len, time_step - node_visited_at_time[u]);
}
}
return longest_cycle_len;
}
}
Python Solution
class Solution:
def longestCycle(self, edges: List[int]) -> int:
longest_cycle_len = -1
time_step = 1
node_visited_at_time = [0] * len(edges)
for current_node in range(len(edges)):
if node_visited_at_time[current_node] > 0:
continue
start_time = time_step
u = current_node
while u != -1 and node_visited_at_time[u] == 0:
node_visited_at_time[u] = time_step
time_step += 1
u = edges[u]
if u != -1 and node_visited_at_time[u] >= start_time:
longest_cycle_len = max(longest_cycle_len, time_step - node_visited_at_time[u])
return longest_cycle_len
Complexity Analysis:-
TIME:-
Time complexity is O(n), where n is the number of nodes in the graph. The outer loop runs for each node, and the inner loop runs at most once for each edge. Therefore, the overall time complexity is O(n).
SPACE:-
Space complexity is O(n), where n is the number of nodes in the graph. We need to store the node_visited_at_time array, which has a length of n. Therefore, the space complexity is O(n).
