Problem Statement:-

Given the root of a Binary Search Tree (BST), return the minimum absolute difference between the values of any two different nodes in the tree.

Link: https://leetcode.com/problems/minimum-absolute-difference-in-bst/description/

Problem Explanation with examples:-

Example 1

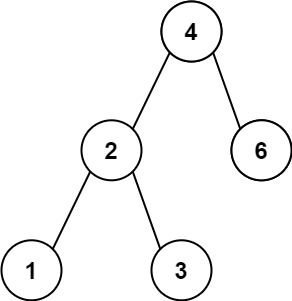
Input: root = [4,2,6,1,3]
Output: 1

Example 2

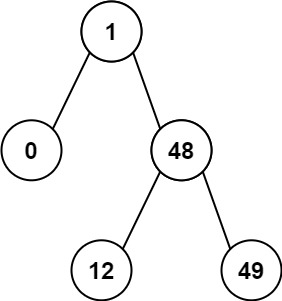
Input: root = [1,0,48,null,null,12,49]
Output: 1

Constraints

• The number of nodes in the tree is in the range [2, 10<sup>4</sup>].

• 0 <= Node.val <= 10<sup>5</sup>

Intuition:-

• Basically going over a DFS-based inorder traversal of the tree and keeping track of the previous value in the inorder traversal.

• At each node, we will check the difference between the current node value and the previous node value and update the minimum difference accordingly.

• Finally, we will return the minimum difference.

Solution:-

• Initialize a variable min_diff to store the minimum difference between any two nodes in the tree. Set it to infinity.

• Initialize a variable prev_val to store the value of the previous node in the inorder traversal. Set it to None.

• Define a function inorder_traversal which takes a node as an argument. This function will perform a DFS based inorder traversal of the tree.

• If the node is None, then return.

• Call inorder_traversal on the left child of the node.

• If prev_val is not None, then update min_diff to be the minimum of min_diff and the absolute difference between the current node value and the previous node value.

• Update prev_val to be the current node value.

• Call inorder_traversal on the right child of the node.

• Call inorder_traversal on the root node.

• Return min_diff.

Code:-

JAVA Solution

class Solution {
    private int minDiff = Integer.MAX_VALUE;
    private Integer prevVal = null;

    public int getMinimumDifference(TreeNode root) {
        inorderTraversal(root);
        return minDiff;
    }

    private void inorderTraversal(TreeNode node) {
        if (node == null) {
            return;
        }

        inorderTraversal(node.left);

        if (prevVal != null) {
            minDiff = Math.min(minDiff, Math.abs(node.val - prevVal));
        }

        prevVal = node.val;

        inorderTraversal(node.right);
    }
}

Python Solution

class Solution:
    def getMinimumDifference(self, root: Optional[TreeNode]) -> int:
        self.min_diff = float('inf')
        self.prev_val = None

        def inorder_traversal(node):
            if node is None:
                return

            inorder_traversal(node.left)

            if self.prev_val is not None:
                self.min_diff = min(self.min_diff, abs(node.val - self.prev_val))

            self.prev_val = node.val

            inorder_traversal(node.right)

        inorder_traversal(root)
        return self.min_diff

Complexity Analysis:-

TIME:-

The time complexity is O(n), where n is the number of nodes in the binary tree. This is because the code performs an inorder traversal of the binary tree, visiting each node exactly once.

SPACE:-

The space complexity is O(h), where h is the height of the binary tree. This is because the space required by the function call stack during recursion is proportional to the height of the tree. In the worst case, where the binary tree is skewed, the height can be equal to the number of nodes in the tree (n), resulting in O(n) space complexity.

References:-

• Traversal

• DFS

Connect with me:-

• Twitter

• Github

• LinkedIn