Problem Statement:-

There are n cities. Some of them are connected, while some are not. If city a is connected directly with city b, and city b is connected directly with city c, then city a is connected indirectly with city c.

A province is a group of directly or indirectly connected cities and no other cities outside of the group.

You are given an n x n matrix isConnected where isConnected[i][j] = 1 if the i<sup>th</sup> city and the j<sup>th</sup> city are directly connected, and isConnected[i][j] = 0 otherwise.

Return the total number of provinces.

Link: https://leetcode.com/problems/number-of-provinces/description/

Problem Explanation with examples:-

Example 1

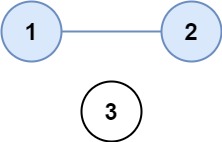
Input: isConnected = [[1,1,0],[1,1,0],[0,0,1]]
Output: 2

Example 2

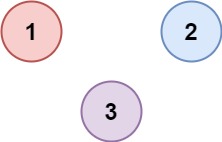
Input: isConnected = [[1,0,0],[0,1,0],[0,0,1]]
Output: 3

Constraints

• 1 <= n <= 200

• n == isConnected.length

• n == isConnected[i].length

• isConnected[i][j] is 1 or 0.

• isConnected[i][i] == 1

• isConnected[i][j] == isConnected[j][i]

Intuition:-

• Simply select a node and traverse as far as possible until you reach a node that has no further connections. This becomes one province.

• Keep track of visited nodes so that you don't visit them again.

• Repeat the above steps for all nodes. DFS is the best way to do this.

Solution:-

• Create a visited array of size n initialized to 0.

• Initialize a variable prov to 0. This will store the number of provinces.

• Define a function dfs which takes a node as input and performs the following: Mark the node as visited. Traverse all the nodes connected to this node and call dfs on them if they are not visited.

• Iterate over all the nodes using a for loop. If the node is not visited, increment prov by 1 and call dfs on that node.

• Return prov.

Code:-

JAVA Solution

class Solution {
    public int findCircleNum(int[][] isConnected) {
        int n = isConnected.length;
        int prov = 0;
        int[] vis = new int[n];

        for (int i = 0; i < n; i++) {
            if (vis[i] == 0) {
                prov += 1;
                dfs(i, isConnected, vis);
            }
        }

        return prov;
    }

    private void dfs(int node, int[][] isConnected, int[] vis) {
        vis[node] = 1;
        for (int nei = 0; nei < isConnected.length; nei++) {
            if (isConnected[node][nei] == 1 && vis[nei] == 0) {
                dfs(nei, isConnected, vis);
            }
        }
    }
}

Python Solution

class Solution:
    def findCircleNum(self, isConnected: List[List[int]]) -> int:
        n = len(isConnected)
        prov = 0
        vis = [0] * n

        def dfs(node):
            vis[node] = 1
            for nei in range(n):
                if isConnected[node][nei] == 1 and vis[nei] == 0:
                    dfs(nei)

        for i in range(n):
            if vis[i] == 0:
                prov += 1
                dfs(i)

        return prov

Complexity Analysis:-

TIME:-

The time complexity is O(n^2), where n is the number of nodes or cities. This is because we iterate over each node in the adjacency matrix in the worst case, and for each node, we check its neighbors. In the worst case, we have to visit all the nodes and their neighbors.

SPACE:-

The space complexity is O(n), where n is the number of nodes or cities. This is because we use an additional array vis of length n to keep track of visited nodes. Additionally, the recursive stack space for the DFS traversal has a maximum depth of n in the worst case.

References:-

• DFS

Connect with me:-

• Twitter

• Github

• LinkedIn