Reorder Routes to Make All Paths Lead to the City Zero

Problem Statement:-

There are n cities numbered from 0 to n - 1 and n - 1 roads such that there is only one way to travel between two different cities (this network form a tree). Last year, The ministry of transport decided to orient the roads in one direction because they are too narrow.

Roads are represented by connections where connections[i] = [a<sub>i</sub>, b<sub>i</sub>] represents a road from city a<sub>i</sub> to city b<sub>i</sub>.

This year, there will be a big event in the capital (city 0), and many people want to travel to this city.

Your task consists of reorienting some roads such that each city can visit the city 0. Return the minimum number of edges changed.

It's guaranteed that each city can reach city 0 after reorder.

Link: https://leetcode.com/problems/reorder-routes-to-make-all-paths-lead-to-the-city-zero/

Problem Explanation with examples:-

Example 1

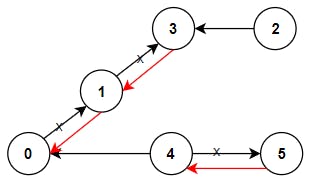
Input: n = 6, connections = [[0,1],[1,3],[2,3],[4,0],[4,5]]
Output: 3
Explanation: Change the direction of edges show in red such that each node can reach the node 0 (capital).

Example 2

Input: n = 5, connections = [[1,0],[1,2],[3,2],[3,4]]
Output: 2
Explanation: Change the direction of edges show in red such that each node can reach the node 0 (capital).

Example 3

Input: n = 3, connections = [[1,0],[2,0]]
Output: 0
Explanation: There are no edges to be reversed as all the edges are already pointing to the direction of the node 0.

Constraints

• 2 <= n <= 5 * 10<sup>4</sup>

• connections.length == n - 1

• connections[i].length == 2

• 0 <= a<sub>i</sub>, b<sub>i</sub> <= n - 1

• a<sub>i</sub> != b<sub>i</sub>

Intuition:-

• We need to find the minimum number of edges that need to be reversed to make the graph connected.

• We can use DFS to traverse each path till the leaf node.

• We can use a visited array to keep track of the visited nodes.

• Starting with node 0, traverse each path till the leaf node and count the number of edges that need to be reversed.

• We can use an adjacency list to store the edges and directions of the edges.

• We can use a negative value to represent the reversed edge and a positive value to represent the original edge.

• Whenever we get a negative value that has not been visited, we can increment the count by 1.

Solution:-

• Initialize an adjacency list to store the edges and directions of the edges.

• Iterate through the edges and add the edges and directions to the adjacency list and the reversed edges and directions to the adjacency list.

• Initialize a visited array to keep track of the visited nodes and set all the elements to False.

• Define a dfs function to traverse each path till the leaf node.

• In dfs function, initialize a change variable to keep track of the number of edges that need to be reversed.

• Set the visited value of the current node to True.

• Iterate through all the adjacent nodes of the current node.

• If the adjacent node is not visited, then we can call the dfs function on the adjacent node and add the number of edges that need to be reversed to the change variable.

• If the adjacent node is a negative value, then we can increment the change variable by 1.

• At the end of dfs function return the change variable.

• Finally, we can return the number of edges that need to be reversed by calling the dfs function on node 0.

Code:-

JAVA Solution

class Solution {
    public int minReorder(int n, int[][] connections) {
        List<Integer>[] al = new ArrayList[n];
        for (int i = 0; i < n; i++) {
            al[i] = new ArrayList<>();
        }
        for (int[] c : connections) {
            al[c[0]].add(c[1]);
            al[c[1]].add(-c[0]);
        }

        boolean[] visited = new boolean[n];
        return dfs(al, visited, 0);
    }

    private int dfs(List<Integer>[] al, boolean[] visited, int fromNode) {
        int change = 0;
        visited[fromNode] = true;
        for (int toNode : al[fromNode]) {
            if (!visited[Math.abs(toNode)]) {
                change += dfs(al, visited, Math.abs(toNode)) + (toNode > 0 ? 1 : 0);
            }
        }
        return change;
    }
}

Python Solution

class Solution:
    def minReorder(self, n: int, connections: List[List[int]]) -> int:
        def dfs(al, visited, from_node):
            change = 0
            visited[from_node] = True
            for to_node in al[from_node]:
                if not visited[abs(to_node)]:
                    change += dfs(al, visited, abs(to_node)) + (1 if to_node > 0 else 0)
            return change

        al = [[] for _ in range(n)]
        for c in connections:
            al[c[0]].append(c[1])
            al[c[1]].append(-c[0])

        print(al)
        visited = [False] * n
        return dfs(al, visited, 0)

Complexity Analysis:-

TIME:-

Time complexity is O(n), where n is the number of nodes in the graph. This is because the code performs a single depth-first search traversal of the graph, visiting each node at most once.

SPACE:-

Space complexity is O(n), where n is the number of nodes in the graph. This is because the code uses an adjacency list to represent the graph, which requires O(n) space, and also uses a boolean array to keep track of visited nodes, which also requires O(n) space. The depth of the recursion is at most n, which means the space used by the function call stack is also O(n).

References:-

• Graph

• DFS

Connect with me:-

• Twitter

• Github

• LinkedIn