Time Needed to Inform All Employees

Problem Statement:-

A company has n employees with a unique ID for each employee from 0 to n - 1. The head of the company is the one with headID.

Each employee has one direct manager given in the manager array where manager[i] is the direct manager of the i-th employee, manager[headID] = -1. Also, it is guaranteed that the subordination relationships have a tree structure.

The head of the company wants to inform all the company employees of an urgent piece of news. He will inform his direct subordinates, and they will inform their subordinates, and so on until all employees know about the urgent news.

The i-th employee needs informTime[i] minutes to inform all of his direct subordinates (i.e., After informTime[i] minutes, all his direct subordinates can start spreading the news).

Return the number of minutes needed to inform all the employees about the urgent news.

Link: https://leetcode.com/problems/time-needed-to-inform-all-employees/description/

Problem Explanation with examples:-

Example 1

Input: n = 1, headID = 0, manager = [-1], informTime = [0]
Output: 0
Explanation: The head of the company is the only employee in the company.

Example 2

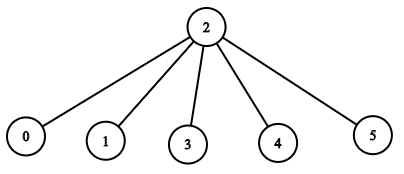
Input: n = 6, headID = 2, manager = [2,2,-1,2,2,2], informTime = [0,0,1,0,0,0]
Output: 1
Explanation: The head of the company with id = 2 is the direct manager of all the employees in the company and needs 1 minute to inform them all.
The tree structure of the employees in the company is shown.

Constraints

• 1 <= n <= 10<sup>5</sup>

• 0 <= headID < n

• manager.length == n

• 0 <= manager[i] < n

• manager[headID] == -1

• informTime.length == n

• 0 <= informTime[i] <= 1000

• informTime[i] == 0 if employee i has no subordinates.

• It is guaranteed that all the employees can be informed.

Intuition:-

• Represent the hierarchy as a tree using an adjacency list.

• Do a BFS traversal of the tree and keep track of the maximum time taken to reach every level.

• Return the maximum time taken to reach the last level.

Solution:-

• Initialize a defaultdict to store the hierarchy of the employees as an adjacency list.

• Traverse the manager array and add the employees as children to their respective managers.

• Initialize a queue and push the headID and the time taken to reach the headID.

• Initialize a variable res to store the maximum time taken to reach the last level.

• While the queue is not empty, pop the first element from the queue.

• Update the res variable with the maximum of res and the time taken to reach the current employee.

• For every employee in the adjacency list of the current employee, push the employee and the time taken to reach the current employee + the time taken to inform the current employee.

• Return the res variable.

Code:-

JAVA Solution

class Solution {
    public int numOfMinutes(int n, int headID, int[] manager, int[] informTime) {
        Map<Integer, List<Integer>> adj = new HashMap<>();
        for (int i = 0; i < n; i++) {
            adj.putIfAbsent(manager[i], new ArrayList<>());
            adj.get(manager[i]).add(i);
        }

        Queue<int[]> q = new LinkedList<>();
        q.offer(new int[]{headID, 0});
        int res = 0;
        while (!q.isEmpty()) {
            int[] current = q.poll();
            int i = current[0];
            int time = current[1];
            res = Math.max(res, time);
            List<Integer> employees = adj.getOrDefault(i, new ArrayList<>());
            for (int emp : employees) {
                q.offer(new int[]{emp, time + informTime[i]});
            }
        }

        return res;
    }
}

Python Solution

class Solution:
    def numOfMinutes(self, n: int, headID: int, manager: List[int], informTime: List[int]) -> int:
        adj = defaultdict(list)
        for i in range(n):
            adj[manager[i]].append(i)

        q = deque([(headID,0)])
        res = 0
        while q:
            i, time = q.popleft()
            res = max(res, time)
            for emp in adj[i]:
                q.append((emp, time + informTime[i]))

        return res

Complexity Analysis:-

TIME:-

The time complexity is O(n), where n is the number of employees. This is because we iterate over each employee once when constructing the adjacency list, and for each employee, we enqueue their subordinates in the queue. In the worst case, we visit each employee once.

SPACE:-

The space complexity is O(n), where n is the number of employees. This is because we store the adjacency list using a HashMap, which can have a maximum of n entries. Additionally, we use a queue to store the employee and their corresponding time, which can have a maximum of n entries in the worst case.

References:-

• BFS

Connect with me:-

• Twitter

• Github

• LinkedIn